Question

What is the area of the shaded region?

(25/1 - 48) cm
(2571 - 30) cm
(2572 - 24) cm
(2571 – 12) cm2

Answer 1

Option (3)

Explanation:

From the figure attached,

Area of the shaded region = Area of circle - (Area of the ΔOAB + Area of ΔOED)

Area of the circle = πr²

= π(5)²

= 25π cm²

Area of ΔOAB = 2(Area of ΔOCB)

AB = 6 cm

OC = 5 - 1 = 4 cm

By applying Pythagoras theorem in ΔOCB,

OB² = OC² + BC²

5² = 4² + BC²

BC² = 25 - 16

BC = √9 = 3 cm

Area of ΔOCB =
`(1)/(2)(OC)(BC)`

=
`(1)/(2)(4)(3)`

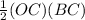
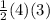
= 6 cm²

Area of ΔAOB = 2(6) = 12 cm²

Area of ΔAOB = Area of ΔDOE = 12 cm²

Area of shaded region = 25π - (12 + 12)

= (25π - 24) cm²

Therefore, Option (3) will be the answer.