Question

What is the completely factored form of the expression 16x2 + 8x + 32?

4(4x2 + 2x + 8)
4(12x2 + 4x + 28)
8(2x2 + x + 4)
8x(8x2 + x + 24)

Answer 1

`8(2x^2+x+4)`

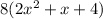
Explanation:

Given expression,

`16x^2 + 8x + 32`

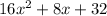
Since,

16 = 2 × 2 × 2 × 2,

8 = 2 × 2 × 2

32 = 2 × 2 × 2 × 2 × 2

LCM(16, 8, 32) = 2 × 2 × 2 = 8,

`\implies 16x^2+8x+32 = 8(2x^2 + x + 4)`

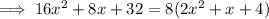
Now,
`1^2 - 4* 2 * 4 \\eq 0`

⇒
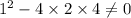
`2x^2 + x + 4` is not a perfect square trinomial,

Hence, the completely factored form of the given expression is,

`8(2x^2 + x+4)`

i.e. THIRD option is correct.

Answer 2

We can give 8 as a common factor and write in parantheses what remains of each term after dividing it by 8. So we have 16x^2 + 8x + 32 = 8*(2x^2 + x + 4). So the answer is C.