Question

Find the point, M, that divides segment AB into a ratio of 5:3 if A is at (-4, -2) and B is at (4, -10).

Answer 1

M(1,-7): Plot the points and then find your slope which is -8/8 or -1. Separate each point into 5 pieces of the left part of the segment and 3 on the right.

Answer 2

Answer: The coordinates of M are ( 1,-7)

Explanation:

Since we know that,

If a point intersects a line having the end points
`(x_1, y_1)` and
`(x_2, y_2)` internally in the ration of m:n,

Then By section formula,

The coordinates of the points are,
`( (m* x_2+n* x_1)/(m+n) , (m* y_2+n* y_1)/(m+n) )`

Here,
`x_1 = -4, x_2 = 4, y_1= -2` and
`y_2 = -10`

While m = 5 and n =3

Therefore coordinates of M are,
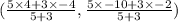
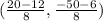
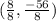
`( (5* 4+3* -4)/(5+3) , (5* -10+3* -2)/(5+3) )`

=
`( (20-12)/(8) , (-50-6)/(8) )`

=
`( (8)/(8) , (-56)/(8) )`

=
`(1, -7 )`