Question

Find the missing length marked with a question mark.
UVW-USR

Answer 1

Given:

`\Delta UVW\sim \Delta USR`

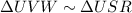
To find:

The missing length marked with a question mark.

Solution:

Let x be the missing value.

We have,

`\Delta UVW\sim \Delta USR`

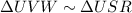
Corresponding sides of similar triangles are proportional, so

`(UV)/(US)=(VW)/(SR)=(UW)/(UR)`

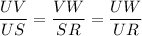
Using this, we get

`(UV)/(US)=(UW)/(UR)`

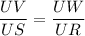
On substituting the values, we get

`(70)/(x)=(55)/(44)`

`(70)/(x)=(5)/(4)`

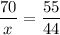
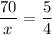
On cross multiplication, we get

`70* 4=5* x`

`280=5x`

`(280)/(5)=x`

`56=x`

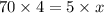
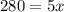
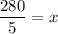
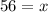
Therefore, the missing length is 56 units.