Question

Hi, no steps/ explications needed. I just need a final answer

Answer 1

First, let's determine the vertex of the parabola, we can do it by using the expression that gives us the coordinate x and y of the vertex, for the x-coordinate we have

`x_V=-(b)/(2a)`

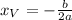
And the y-coordinate

`y_V=-(\Delta)/(4a)`

And the vertex is

`V=(x_V,y_V)`

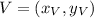
Applying the formula

`\begin{gathered} x_V=(-12)/(2\cdot(-2))=3 \\ \\ y_V=(144-4\cdot(-2)\cdot(-19))/(4\cdot(-2))=(-8)/(8)=-1 \end{gathered}`

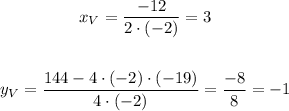
The vertex is

`V=(3,-1)`

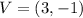
Let's plot two points to the right of the vertex, which means x > 3, I'll pick x = 4 and x = 5

`\begin{gathered} f(x)=-2x^2+12x-19 \\ \\ f(4)=-2\cdot4^2+12\cdot4-19=-3 \\ \\ f(5)=-2\cdot5^2+12\cdot5-19=-9 \end{gathered}`

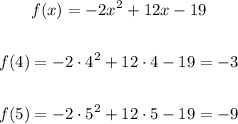
Then two points at the right of the vertex are

`\begin{gathered} (4,-3) \\ \\ (5.-9) \end{gathered}`

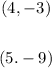
And at the left, I'll pick 0 and 1

`\begin{gathered} f(0)=-19 \\ \\ f(1)=-9 \end{gathered}`

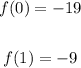
Therefore the points are

`\begin{gathered} (0,-19) \\ \\ (1,-9) \end{gathered}`

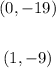
Final answer:

`\begin{gathered} \text{ vertex:} \\ V=(3,-1) \\ \\ \text{ right points:} \\ (4,-3) \\ \\ (5,-9) \\ \\ \text{ left points:} \\ (0,-19) \\ \\ (1,-9) \end{gathered}`