Question

Match each equation on the right side to its solution on the left side. Some answer options on the left side will be used more than once. X = all real numbersno solution x = 0 9 + 7x – 12 = 3x + 5 – 4(2 – x) 12 + 7x – 9 = 3x + 5 – 4(2 - x) 4 – 9x = 3 – 10x - (7 - x) 5(3 – x) + 8x = 3(x + 5) 5(3 - x) = 3(× + 5 )

Answer 1

9 + 7x – 12 = 3x + 5 – 4(2 – x) Solution: x = all real numbers

12 + 7x – 9 = 3x + 5 – 4(2 - x) Solution: no solution

4 – 9x = 3 – 10x - (7 - x) Solution: no solution

5(3 – x) + 8x = 3(x + 5) Solution: x = all real numbers

5(3 - x) = 3(× + 5 )​ Solution: x = 0

Step-by-step explanation:

To match the expressions, we solve for x in each case.

Equation 1. 9 + 7x – 12 = 3x + 5 – 4(2 – x)

Expanding both sides of the equation gives

`\begin{gathered} 9+7x-12=3x+5-8+4x \\ \end{gathered}`

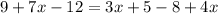
simplifying gives

`7x-3=-3+7x`

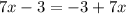
adding 3 to both sides gives

`7x=7x`

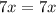
which has infinitely many solutions (meaning all real numbers)

Equation 2. 12 + 7x – 9 = 3x + 5 – 4(2 - x)

Expanding both sides gives

`12+7x-9=3x+5-8+4x`

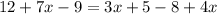
simplifying gives

`3+7x=7x-3`

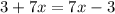
subtracting 7x from both sides gives

`3=-3`

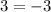
which cannot be true, and therefore, the equation has no solutions.

Equation 3. 4 – 9x = 3 – 10x - (7 - x)

Expanding both sides of the equation gives

`4-9x=3-10x-7+x`

simplifying gives

`4-9x=-9x-4`

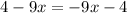
adding 9x to both sides gives

`4=-4`

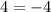
which cannot be true, and therefore, the equation has no solutions.

Equation 4. 5(3 – x) + 8x = 3(x + 5)

Expanding both sides of the equation gives

`15-5x+8x=3x+15`

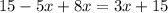
simplifying gives

`15+3x=3x+15`

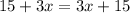
which has infinitely many solutions (any value of x you pick will satisfy the equation above)

Equation 5. 5(3 - x) = 3(x + 5 )​

Expanding both sides of the equation gives

`15-5x=3x+15`

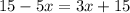
subtracting 15 from both sides gives

`-5x=3x`

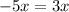
which has no solutions (no value of x you pick will satisfy the equation).

Hence to summarise, the answers are the following.

9 + 7x – 12 = 3x + 5 – 4(2 – x) Solution: x = all real numbers

12 + 7x – 9 = 3x + 5 – 4(2 - x) Solution: no solution

4 – 9x = 3 – 10x - (7 - x) Solution: no solution

5(3 – x) + 8x = 3(x + 5) Solution: x = all real numbers

5(3 - x) = 3(× + 5 )​ Solution: x = 0