Question

Catarina and Tom want to buy a rug for a room that is 8 by 12. They want to leave an even strip of flooring uncovered around the edges of the room. How wide a stip will have if they buy a rug with an area of 32 square feet

Answer 1

The length of the strip is 4ft

Step-by-step explanation:

Given

Room dimension: 8 by 12

Rug Area: 32

Required

Determine the width of the strip

Since it is an even strip. Represent the width with w.

So, the rug area
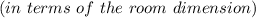`(in\ terms\ of\ the\ room\ dimension)` is:

`Area = (8 - w) * (12 - w)`

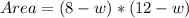
Substitute 32 for Area

`32 = (8 - w) * (12 - w)`

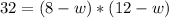
Expand

`32 = 8(12 - w) -w(12 - w)`

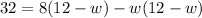
Open brackets

`32 = 96 - 8w -12w + w^2`

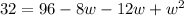
Collect Like Terms

`w^2 - 12w - 8w -32 + 96 = 0`

`w^2 - 20w+64 = 0`

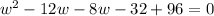
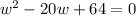
Expand

`w^2 - 16w - 4w + 64 = 0`

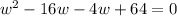
Factorize

`w(w - 16) - 4(w - 16) = 0`

`(w - 4)(w - 16) = 0`

`w - 4 = 0\ \ or\ w-16=0`

`w = 4\ \ or\ w=16`

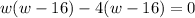
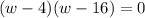
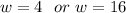
But w can't be greater than the any of the dimension of the room (8 or 12).

So:

`w = 4`

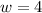
Hence, the length of the strip is 4ft