Question

Solve the following equation on the interval [0, 360°]:3sin 2x = -2cos22x

Answer 1

We have to solve the following

`3\sin (2x)=-2\cos ^2(2x)`

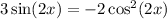
We need to find a trigonometric identity

`\cos ^2(2x)=1-\sin ^2(2x)`

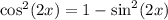
then

`\begin{gathered} 3\sin (2x)=-2\cdot(1-\sin ^2(2x)) \\ 3\sin (2x)=-2+2\sin ^2(2x) \\ \end{gathered}`

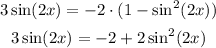
we can rewrite this as

`2\sin ^2(2x)-3\sin (2x)-2=0`

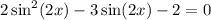
We can make the following substitution

`\begin{gathered} u=\sin (2x) \\ \Rightarrow2u^2-3u-2=0 \end{gathered}`

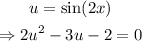
Now, solve with the quadratic formula

`\begin{gathered} x_(1,\: 2)=(-b\pm√(b^2-4ac))/(2a) \\ \end{gathered}`
`u_(1,\: 2)=(-\left(-3\right)\pm√(\left(-3\right)^2-4\cdot\:2\left(-2\right)))/(2\cdot\:2)`
`u_1=(-\left(-3\right)+5)/(2\cdot\:2),\: u_2=(-\left(-3\right)-5)/(2\cdot\:2)`

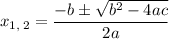
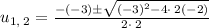
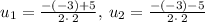
So, we get there are two values for u

`u=2,\: u=-(1)/(2)`

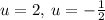
Now, let's substitute back

`\begin{gathered} u=\sin (2x) \\ \Rightarrow\sin \mleft(2x\mright)=-(1)/(2),\: \sin \mleft(2x\mright)=2 \end{gathered}`

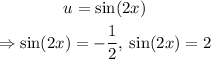
we're almost done!

Now, let's find x for each case

`\begin{gathered} \sin \mleft(2x\mright)=-(1)/(2) \\ 2x=(7\pi)/(6)+2\pi n,\: 2x=(11\pi)/(6)+2\pi n \\ x=(7\pi)/(12)+\pi n,\: x=(11\pi)/(12)+\pi n \end{gathered}`

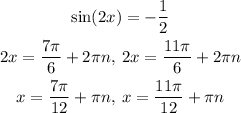
for the other one there is no solution

`\sin \mleft(2x\mright)=2\quad \colon\quad \mathrm{No\: Solution\: for}\: x\in\mathbb{R}`

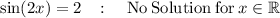
So the answer in degrees from 0° to 360° is:

`\begin{gathered} x=105^(\circ)+180^(\circ\: )n,\: x=165^(\circ)+180^(\circ\: )n \\ x=105^(\circ\: ),165^(\circ),285^(\circ\: ),345^(\circ\: ) \end{gathered}`

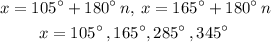
Answer: 105°, 165°, 285° and 345°