Question

carly bought a new house for $125,000. the value of the house appreciates approximately 3.5% each year. what will be the value of the house after 10 years?

Answer 1

We have to determine the value of a house after 10 years. We know that the present value of the house is $125,000 and that the value increases 3.5% each year. Formula is: FV = PV * ( 1 + r )^t, where FV is the future value, PV is the present value, r = 3.5% = 0.035 and t = 10 years. FV = 125,000 *( 1.035 )^10 = 125,000 * 1.4105; FV = $176,324.85 ( $ 176,325 to the nearest dollar ). Answer: The value of the house after 10 years will be $176,325.

Answer 2

Value of the house after 10 years is $176325 .

Explanation:

The exponential increases function is given by

`y = a (1 + r)^(t)`

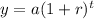
Where a is the initial value , r is the rate of interest in the decimal form and t is the time in years .

As given

Carly bought a new house for $125,000. the value of the house appreciates approximately 3.5% each year.

a = $125000

3.5% is written in the decimal form

`= (3.5)/(100)`

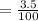
= 0.035

r = 0.035

t = 10 years

Put all the values in the formula

`y = 125000 (1 + 0.035)^(10)`

`y = 125000(1.035)^(10)`

`y = 125000* 1.4106`

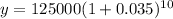
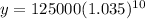
y = $ 176325

Therefore the value of the house after 10 years is $176325 .