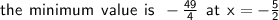Step-by-step explanation
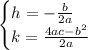
The vertex of Parabola is the maximum/minimum point depending on the value of a.
h-value
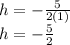
k-value
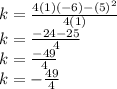
The minimum value is the value of k. Therefore the minimum value is - 49/4 at x = -5/2.
This is Calculus method. We simply differentiate the function then substitute y' = 0.
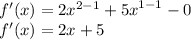
Substitute f'(x) = 0
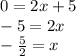
Substitute x = -5/2 in the original equation.
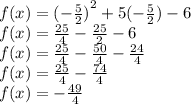
Answer