Step-by-step explanation
From the statement, we know that the height h (in feet) of an object is given by the following function of time t (in seconds):
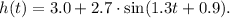
a. The velocity of the object is obtained by taking the first derivative:
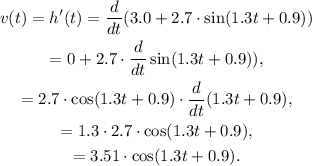
Evaluating the function for t = 4 seconds, we get:
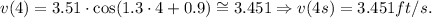
b. The first instant after t = 0 when the velocity is 0 is obtained by solving for t the equation:
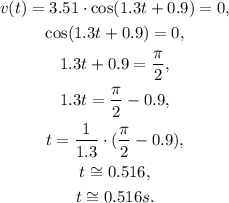
c. The next instant in time when the velocity is 0 is obtained by solving for t the following equation:
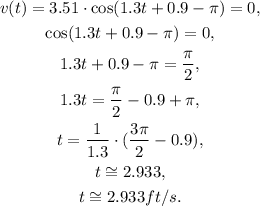
d. The acceleration of the object is obtained by taking the first derivative of the velocity:
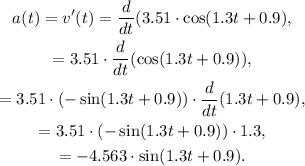
When the height is h = 4, we have:
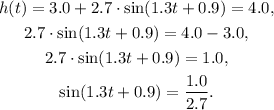
The acceleration when the height is h(t) = 1.0 is:

Answer
• a. 3.451 ft/s
,
• b. 0.516 s
,
• c. 2.933 s
,
• d. -1.690 ft/s²