Question

-6. Given: 9w2 – 8w +6w4 – 5a) Write the polynomial in descending order.b) What is the degree of the polynomial?c) What is the leading coefficient?d) What is the coefficient of w?e) Evaluate the expression if w=2.

Answer 1

Given:

`9w^2-8w+6w^4-5`

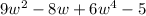
a)

We need to write the polynomial in descending order.

Recall that descending order is basically when the power of a term decreases for each succeeding term.

The power of w decreasing from 4 to 0 is the descending order

Answer:

`6w^4+9w^2-8w-5`

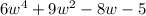
b)

We need to find the degree of the polynomial.

Recall that the degree of the polynomial is the greatest power of the variable.

The variable of the given polynomial is w.

The greatest power of the variable w in the given polynomial is 4.

Answer:

The degree of the polynomial is 4.

c)

We need to find the leading coefficient.

Recall that the leading coefficient is the coefficient of the term of the highest degree in a given polynomial.

The highest degree in a given polynomial is 4.

`\text{ The term of the highest degree in a given polynomial }6w^4.`

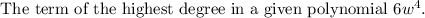
The coefficient of the term of the highest degree in a given polynomial is 6.

Answer:

The leading coefficient is 6.

d)

We need to find the coefficient of w.

Recall that the coefficient of w is the number multiplied by the variable.

In the given polynomial w is multiplied by -8.

Answer:

The coefficient of w is -8.

e)

We need to evaluate the expression if w=2.

Substitute w=2 in the given polynomial.

`9(2)^2-8(2)+6(2)^4-5`

`=9(4)-8(2)+6(16)-5`

`=36-16+96-5`

`=111`

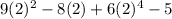
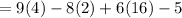
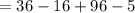
Answer:

The given expression is 111 if w =2.