Question

NEED HELP 50 POINTS TO WHOEVER CAN ANSWER

Eric is driving to Los Angeles. Suppose that the distance to his destination (in miles) is a linear function of his total driving time (in minutes). Eric has 65 miles to his destination after 35 minutes of driving, and he has 44 miles to his destination after 63 minutes of driving. How many miles will he have to his destination after 79 minutes of driving?

Answer 1

32 Miles

Explanation:

Okay so this will take a moment:

Let's set up the following variables:

d = total distance of the trip

v = some rate of velocity/travel

Note: t is not a variable here as it would denote time, but we know the time, so rate of travel as a variable is next best.

With those variables, we can set up 3 equations as follows:

d - 35v = 65

d - 63v = 44

d - 79v = x

The equations being read as:

[total distance] - [time and rate of travel] = [distance remaining]

Now if we restructure each of those equations, you will have:

d = 35v + 65

d = 63v + 44

d = 79v + x

Now you can treat this like a system of equations. First we will solve for the variable: v

Since the total distance remains the same, we can set up the following equation:

• 35v + 65 = 63v + 44

subtract 35v from both sides

• 65 = 28v + 44

subtract 44 from both sides

• 21 = 28v

Now if we turn it around:

• 28v = 21

The common factor of both of these numbers is 7, so divide both by 7:

• 4v = 3

Therefore:

• v =
  `(3)/(4)`

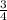
That was a lot. NOW that you know the value of v, you can find the total distance that Eric needs to travel, so plug it into one of the equations:

d = 35(
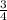`(3)/(4)` ) + 65

Solve, and you get:

d = 91.25 miles =
`(365)/(4)` miles

Now that you know what the variables: v and d , you can solve for x in the other equation: d = 79v + x

`(365)/(4)` = 79 (
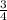`(3)/(4)` ) + x

Multiply.

`(365)/(4)` =
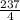`(237)/(4)` + x

Subtract.

`(365)/(4)` -
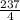`(237)/(4)` = x

Simplify.

x =
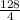`(128)/(4)` = 32

Voila! 32 Miles to go! Good Luck!