Question

write the equation for an exponential function, in the forms y = a x b^x, whose graph passes through the coordinate points (1, 7.5) and (3, 16.875).

Answer 1

The the required exponential function is
`y=5(1.5)^x`.

Explanation:

The equation for an exponential function, in the forms

`y=ab^x`

It is given that passes through the coordinate points (1, 7.5) and (3, 16.875). It means the given function must be satisfied by these points.

`7.5=ab^1`

`7.5=ab` ....(1)

`16.875=ab^3` ..... (2)

Divide equation (2) by equation (1).

`(16.875)/(7.5)={ab^3}{ab}`

`2.25=b^2`

`b=1.5`

The value of b is 1.5. Substitute b=1.5 in equation (1).

`7.5=a(1.5)`

Divide both sides by 1.5.

`a=5`

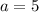
Therefore the required exponential function is
`y=5(1.5)^x`.

Answer 2

y = abˣ
(a ≠ 0, b ≠ 0)

(1, 7.5)
x = 1
y = 7.5
↓
7.5 = ab

(3, 16.875)
x = 3
y = 16.875
↓
16.875 = ab³

7.5 = ab
b b
7.5/b = a

16.875 = ab³
b³ b³
16.875/b³ = a

7.5/b = 16.875/b³
7.5/b(b³) = 16.875/b³(b³)
7.5b² = 16.875
7.5 7.5
b² = 2.25
√(b²) = √(2.25)
b = 1.5

a = 7.5/b
a = 7.5/1.5
a = 5

y = 5(1.5)ˣ