Question

50 points for answer.

Three vertices of parallelogram ABCD are A(2,6), B(2,2) and D(4,4). Find the coordinates of the remaining vertex.

Answer 1

Point c: (4,0) hope this helps you

Answer 2

Point C: (4, 0)

Explanation:

Parallelograms are quadrilaterals with two pairs of parallel sides, this means they will have the same slope between two line segments.

point slope form between two points: y - y1 = m (x - x1)

point A (2, 6) and D (4,4):

slope: point form, 6 - 4 = m(2 - 4)

2 = -2m

m (slope) =
`\frac {2}{-2}` =
`\frac {Change in X position}{ Change in Y position}`

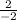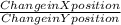
now that you know the change in position, apply this to vertice B to get the position of the final vertice.

B(2, 2)

C (2 +2, 2-2) = C(4, 0)

The final position of C vertice for parrallelogram A(2,6), B(2,2), D(4,4) will be C(4,0)