Question

segment CD has endpoints at C(0, 3) and D(0, 7). If the segment is dilated by a factor of 3 about point C, what is the length of the image of segment CD ?1242116

Answer 1

Given:

C(0, 3) and D(0, 7)

Scale factor of dilation = 3

Lt's find the length of CD if it is dilated about point C.

To find the length, apply the formula:

`L=r√((x2-x1)^2+(y2-y1)^2)`

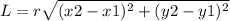
Where:

r is the scale factor = 3

L is the length of segment CD.

(x1, y1) ==> (0, 3)

(x2, y2) ==> (0, 7)

Thus, we have:

`\begin{gathered} CD=3√((0-0)^2+(7-3)^2) \\ \\ CD=3(√(4^2)) \\ \\ CD=3(4)=\text{ 12} \\ \end{gathered}`

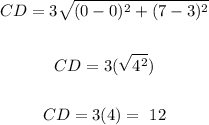
Therefore, the length of CD is 12

ANSWER:

12