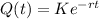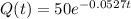Answer:
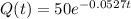
Explanation:
A certain radioactive material is known to decay at a rate proportional to the amount present.
This means that the situation can be described by the following differential equation:

In which r is the decay rate.
Solving the differential equation by separation of variables, we have that:
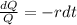
Integrating both sides:

In which K is the integrative constant.
Applying the exponential to both sides, to remove the ln, we get:
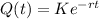
In which K is the initial amount present.
Initially there is 50 mg/L
This means that
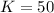 .
.
After 2 hours it is observed that the material has lost 10 percent of its original concentration
This means that
 . So
. So
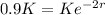

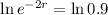
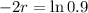
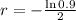
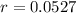
So