Notice the following pattern:

Then, the function that gives us the miles the motorcyclist drives in a time t (t in hours) is
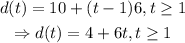
a) We need to find t such that
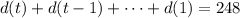
Notice that:

Then, the answer is 8 hours.
b)
We can continue the pattern given above and obtain
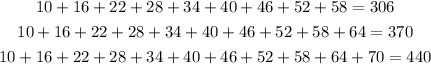
Then, the answer is the 11th hour
Solving the problem using summation notation:

Therefore
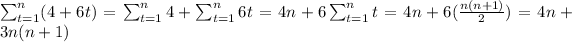
Thus,
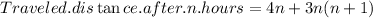
In the last step, we used the Gauss sums of consecutive integers., which states that
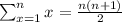
The formula to know how many miles we have traveled after n hours is 4n+3n(n+1)