Question

At one university, the mean distance commuted to campus by students is 19.0 miles, with a standard deviation of 4.2 miles. Suppose that the commutedistances are normally distributed. Complete the following statements.(a) Approximately 95% of the students have commute distances between ? milesand ? miles(b) Approximately ? of the students have commute distances between 6.4 miles and 31.6 miles.

Answer 1

Part a.

From the given information, we know that the mean and standard deviation are, respectively,

`\begin{gathered} \mu=19 \\ \sigma=4.2 \end{gathered}`

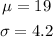
From the 68-95-99 rule, we know that approximately 95% falls between 2 standard deviation of the mean, that is,

`-2=(x-19)/(4.2)...(A)`

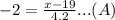
and

`2=(x-19)/(4.2)...(B)`

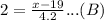
From equation (A), we have

`x-19=-8.4`

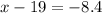
then

`x=10.6`

Now, from equation (B), we get

`\begin{gathered} x-19=8.4 \\ then \\ x=27.4 \end{gathered}`

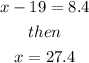
Therefore, the answer for part a is: Approximately 95% of the students have commute between 10.6 and 27.4 miles

Part b.

In this case, we need to find the z score value for 6.4 miles and 31.6 miles and then obtain the corresponding probabilty from the z-table.

For 6.4 miles, the z score is

`z=(6.4-19)/(4.2)=-3`

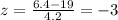
and for 31.6 miles, the z score is

`z=(31.6-19)/(4.2)=3`

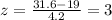
Now, we need to find the corresponding probability between z=-3 and z=3, which is 0.9973

Therefore, the answer for part b is: Approximately. 0.9973 of the students have commute distances between 6.4 miles and 31.6 miles