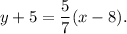Question

A line contains the point (8, –5). If the slope of the line is 5/7, write the equation of the line using point-slope form.

Answer 1

Answer: The required equation of the line is
`y+5=(5)/(7)(x-8).`

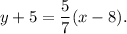
Step-by-step explanation: Given that a line contains the point (8, -5) and the slope of the line is {tex]\dfrac{5}{7}.[/tex]

We are to write the equation of the line using point-slope form.

We know that

the equation of a line with slope m and passing through the point (a, b) is given by

`y-b=m(x-a).`

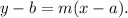
For the given line, we have

`m=(5)/(7),~~~(a,b)=(8,-5).`

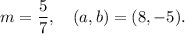
Therefore, the equation of the line will be

`y-b=m(x-a)\\\\\Rightarrow y-(-5)=(5)/(7)(x-8)\\\\\Rightarrow y+5=(5)/(7)(x-8).`

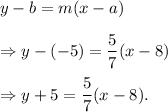
Thus, the required equation of the line is
`y+5=(5)/(7)(x-8).`

Answer 2

Answer:
`(y+5)=(5)/(7)(x-8)`

Explanation:

The point slope form of a line having slope m and point (a,b) is given by :-

`(y-b)=m(x-a)`

Given: A line contains the point = (8, –5)

The slope of the line =
`(5)/(7)`

Now, the point slope form of a line having slope
`(5)/(7)` and point (8,-5) is given by :-

`(y-(-5))=(5)/(7)(x-8)\\\\\Rightarrow\ (y+5)=(5)/(7)(x-8)`

Hence, the equation of the line =
`(y+5)=(5)/(7)(x-8)`