Question

(a)Profit function P(x) (b)Find the number items which need to sold in order to maximize profit. (c)Find maximum profit. (d)The price to charge per item order to maximize profit. (e)Find and interpret break even point .

Answer 1

Step-by-step explanation:

• The cost to produce x T-shirts: C(x)=2x+26, x≥0

,

• The price-demand function per shirt: P(x)=30-2x, 0≤x≤15.

The revenue generated from the sale of x T-shirts will be:

`R(x)=x* P(x)=x(30-2x)`

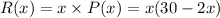
The profit earned will be:

Next, we maximize the profit.

This is done by taking the derivative of P(x), setting it equal to 0 and solving for x.

`\begin{gathered} P^(\prime)(x)=-4x+28 \\ \text{Set P'(x)=0} \\ -4x+28=0 \\ 4x=28 \\ x=7 \end{gathered}`

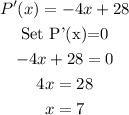
The number of items that need to be sold to maximize profit, x=7.

Maximum Profit

Substitute x=7 into P(x) to find the maximum profit.

`\begin{gathered} P(x)=-2x^2+28x-26 \\ \implies P(7)=-2(7)^2+28(7)-26=-98+196-26 \\ =-98+196-26 \\ =72 \end{gathered}`

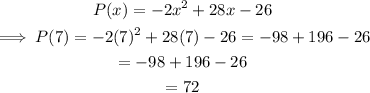
The maximum profit is $72.

Price to charge

When x=7

`\begin{gathered} P(x)=30-2x \\ P(7)=30-2(7)=30-14=16 \end{gathered}`

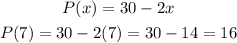
The company needs to charge $16 per item to maximize profit.

Break-Even Point

To break even, the cost must be equal to revenue.

`\begin{gathered} R(x)=C(x) \\ x(30-2x)=(2x+26) \\ -2x^2+30x-2x-26=0 \\ -2x^2+28x-26=0 \\ 2x^2-28x+26=0 \\ 2x^2-2x-26x+26=0 \\ 2x(x-1)-26(x-1)=0 \\ (2x-26)(x-1)=0 \\ 2x-26=0\text{ or }x-1=0 \\ x=13\text{ or }x=1 \end{gathered}`

If 1 T-shirt is sold, the company breaks even.