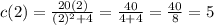To determine when the concentration will be 0.5 mg/l we must replace that value on the equation provided by the exercise and clear the equation for t.
To complete the solution we can subtract 20t from both sides and we obtain a trinomial of the form ax2+bx+c
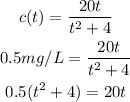
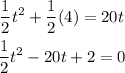
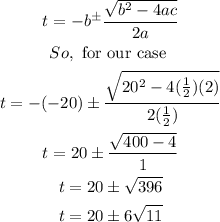
Thus,
a. The concentration will be 0.5 mg/L when they have passed approximately 39.90hours or 0.10hours.
b.To complete the table we have to replace each value of t in the equation of c(t). For example, when t is equal to 2