Question

8. A pole is supported by two wires, one on each side, going in opposite directions. The wires are 14 feet and 17 feet long. If the wires are to be secured to the ground 22 feet from each other what angle must the 14-foot long wire moke with the ground?

Answer 1

Let's make a diagram to visualize the problem.

As you can observe in the diagram above, the problem is asking for the angle between the 14-foot long wire and the ground. In order to find the angle, we have to use the law of cosines.

`c^2=a^2+b^2-2ab\cdot\cos x`

Where c = 17, a = 14, and b = 22. Let's replace these values and solve for x.

`\begin{gathered} 17^2=14^2+22^2-2\cdot14\cdot22\cdot\cos x \\ 289=196+484-616\cdot\cos x \\ 289=680-616\cdot\cos x \\ 289-680=-616\cdot\cos x \\ -391=-616\cdot\cos x \\ \cos x=(-391)/(-616) \\ x=\cos ^(-1)((391)/(616)) \\ x\approx50.6 \end{gathered}`

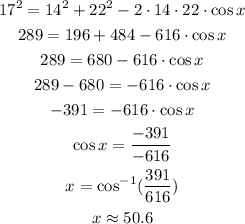
Therefore, the angle that the 14-foot long wire forms with the ground is 50.6°.