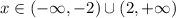The given inequality is:
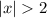
Since this is an absolute value inequality, separate the inequality into possible cases using the definition of an absolute value:
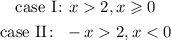
For the case I, find the intersection:
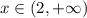
For case II, solve the first inequality:
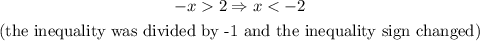
Hence, the set of inequalities for case II becomes:

Find the intersection:
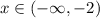
Find the union of the two solutions to get the solution of the inequality: