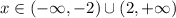Question

Problem 5 Solve the following inequality: |×|>2. Put your answer in interval notation.

Answer 1

The given inequality is:

`|x|>2`

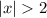
Since this is an absolute value inequality, separate the inequality into possible cases using the definition of an absolute value:

`\begin{gathered} \text{case I}\colon x>2,x\geqslant0 \\ \text{case II}\colon\; -x>2,x<0 \end{gathered}`

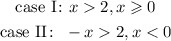
For the case I, find the intersection:

`x\in(2,+\infty)`

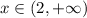
For case II, solve the first inequality:

`\begin{gathered} -x>2\Rightarrow x<-2 \\ (\text{the inequality was divided by -1 and the inequality sign changed)} \end{gathered}`

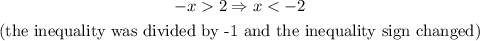
Hence, the set of inequalities for case II becomes:

`x<-2,x<0`

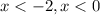
Find the intersection:

`x\in(-\infty,-2)`

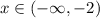
Find the union of the two solutions to get the solution of the inequality:

`x\in(-\infty,-2)\cup(2,+\infty)`