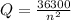Question

The volume, Q, of a sound is inversely proportional to the square of the distance n, in meters, from the source of the sound. A sound is heard at 75 decibels at a distance of 22 meters from its source. Write a formula for Q as a function of n, including finding the value of any unknown constants. Q = _______

Answer 1

Step 1. Define the variables for the formula.

Q --> Volume of the sound

n --> Distance in meters from the source of the sound

Step 1. Since Q is inversely proportional to the square of the distance n, the formula we will use for inverse proportionality is:

`Q=(a)/(n^2)`

Where a is a constant of proportionality.

Step 2. Find the value of constant a.

We are given the following known values:

''A sound is heard at 75 decibels at a distance of 22 meters from its source''

here, the values for Q and n are:

`\begin{gathered} Q=75 \\ n=22 \end{gathered}`

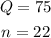
Ans we need to substitute them into our inverse proportionality formula in order to find a:

`\begin{gathered} Q=(a)/(n^2) \\ 75=(a)/(22^2) \end{gathered}`

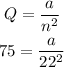
Solving for a:

`\begin{gathered} 75*22^2=a \\ 75*484=a \\ 36,300=a \end{gathered}`

The value of the constant a is 36,300.

Step 3. Substitute the value of the constant into the formula:

`\begin{gathered} Q=(a)/(n^2) \\ Q=(36300)/(n^2) \end{gathered}`

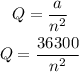
This is the formula for Q as a function of n.

Answer:

`Q=(36300)/(n^2)`