Question

Determine the magnitude of the resultant force and its direction using both the parallelogram and Cartesian vector notation methods. The direction of the resultant force is measured counter-clockwise from the positive x-axis. Draw the resultant force in the Cartesian coordinate system.F1= 600 N, F2= 900 N, β1 = 50 degree, and β2 = 40 degree.

Answer 1

F = 1494.52 N, θ = 44º

Step-by-step explanation:

For the sum of vectors by the parallelogram method, see attached, the vectors are drawn, the parallelogram is completed and a vector is drawn from the origin of the two vectors to the end point of the rectangle, this is the resulting vector.

The attachment shows this roughly.

For the Cartesian coordinate method, each vector is decomposed into its components, they are added algebraically and then the resulting vector is composed in the form of a module and angles

we use trigonometry to decompose the vectors.

The coordinate system can be seen in the attachment

sin θ = y / R

cos θ = x / R

y = R sin θ

x = R cos θ

Vector 1

module F₁ and angle β₁ = 50

sin 50 =
`(F_(1y) )/(F_1)`

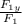
cos 50 =
`(F_(1x) )/(F_1)`

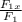
`F_(1y)` = F₁ sin 50

F₁ₓ = F₁ cos 50

F_{1y} = 600 sin 50 = 459.63 N

F₁ₓ = 600 cos 50 = 385.67 N

Vector 2

modulus F₂ = 900N, angle β₂ = 40

F_{2y} = 900 sin 40 = 578.51 N

F₂ₓ = 900 cos 40 = 689.44 N

we find the resultant of each component

F_{y} =F_{1y} + F_{2y}

F_{y} = 459.63 + 578.51

F_{y} = 1038.14 N

Fₓ = F₁ₓ + F₂ₓ

Fₓ = 385.67 + 689.44

Fₓ = 1075.11 N

We use the Pythagorean theorem to find the modulus of the resultant

F = Fₓ² +
`F_(y)^2`

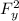
F = √(1075.11² + 1038.14²)

F = 1494.52 N

we use trigonometry for the angle

tan θ = F_y / Fₓ

θ = tan⁻¹ (F_y / Fₓ)

θ = tan⁻¹ (1038.14 / 1075.11)

θ = 44º