Answer:
y =

Explanation:
As given , y' = 3y - 2y²
⇒y' - 3y = -2y²
Divide by y² in the above equation
⇒
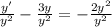
⇒
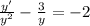 ........(1)
........(1)
Now , let
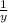 = u
= u
⇒-
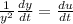
⇒-

∴ equation (1) becomes
-
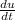 - 3u = -2
- 3u = -2
⇒
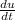 + 3u = 2
+ 3u = 2
It is a linear differential equation
Now,
Integrating factor = I.F =
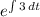 =
=
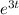
∴ The solution becomes
u.(I.F) =
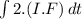 + C
+ C
⇒u.(
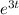 ) =
) =
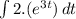 + C
+ C
⇒u.(
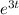 ) =
) =
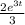 + C
+ C
⇒u =
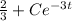
As
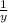 = u
= u
⇒
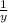 =
=
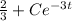
⇒ y =
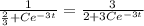
⇒ y =
