We can express the groth of the bacterias by the following expression:
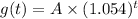
Where A is the initial amount of bacteria, we want to know how many hours we need to double the initial amount. So we want to solve:
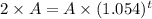
Lets use natural logaritm to help to solve the question:
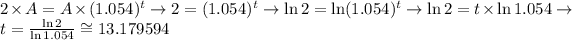
So, we need 13.18 hours to double our initial amount.