Question

The Ostwald process is used commercially to produce nitric acid, which is, in turn, used in many modern chemical processes. Inthe first step of the Ostwald process, ammonia is reacted with oxygen gas to produce nitric oxide and water.What is the maximum mass of H, that can be produced by combining 66.8 g of each reactant?4NH,(g) + 502(9) — 4 NO(g) + 6H2O(g)mass:gHO

Answer 1

The maximum amount of water produced is 45.09 g H20

Step-by-step explanation

Given data

The mass of ammonia = 66.8g

The mass of oxygen = 66.8 g

To find the maximum amount of water produced in grams, follow the steps below

Step 1: Write the balanced equation of the reaction

`\text{ 4NH}_(3(g))+\text{ 5O}_(2(g))\rightarrow4NO_((g))\text{ + 6H}_2O_((g))`

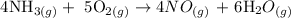
From the above reaction, you will see that 4 moles of ammonia and 5 moles of oxygen produce 4 moles of nitrogen oxide and 6 moles of water

Step 2: Find the number of moles in each of the reactants using the below formula

`\text{ Mole = }\frac{\text{ mass}}{\text{ molar mass}}`

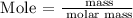
Recall, that the molar mass of ammonia is 17.031 g/mol and the molar mass of oxygen is 32 g/mol

For ammonia

`\begin{gathered} \text{ Mole of NH}_3\text{ = }(66.8)/(17.031) \\ \text{ Mole of NH}_3\text{ = 3.922 moles} \end{gathered}`

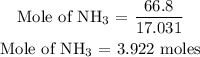
For oxygen

`\begin{gathered} \text{ Mole of O}_2\text{ = }(66.8)/(32) \\ \text{ Mole of O}_2\text{ = 2.0875 moles} \end{gathered}`

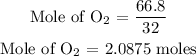
Step 3: Find the limiting reactant of the reaction.

To find the limiting reactant, divide the number of moles by the coefficient of each reactant. Hence, the reactant with the least number of moles becomes the limiting reactant.

`\begin{gathered} \text{ For NH}_3 \\ \text{ The coeffcient of ammonia in the reaction is 4. Hence, we have} \\ (3.922)/(4)\text{ = 0.9805 mole/wt} \\ \\ \text{ For O}_2 \\ \text{ The coefficient of oxygen in the reaction is 5. Hence, we have} \\ (2.0875)/(5)\text{ = 0.4175 mole/wt} \end{gathered}`

From the above calculations, you will see that oxygen has the least number of moles per wt, hence, oxygen is the limiting reactant

Step 4: Find the number of moles of water using a stoichiometry ratio.

To find the moles of water, we use the moles of the limiting reactant

Recall, that the mole of oxygen is 2.0875 moles

From the reaction, 5 moles of oxygen give 6 moles of water

Let x represents the number of moles of water

Mathematically, we have

`\begin{gathered} 5\text{ moles of O}_2\text{ }\rightarrow\text{ 6 moles of H}_2O \\ 2.0875\text{ moles of O}_2\rightarrow\text{ x moles of H}_2O \\ \text{ 5}\rightarrow\text{ 6} \\ 2.0875\rightarrow x \\ cross\text{ multiply} \\ 5* x\text{ = 6 }*2.0875 \\ 5x\text{ = 12.525} \\ \text{ Divide both sides by 5} \\ \text{ }(5x)/(5)\text{ = }(12.525)/(5) \\ x\text{ = 2.505 moles} \end{gathered}`

Hence, the number of moles in water is 2.505 moles

Step 5: Find the mass of water in grams using the below formula

`\text{ Mole = }\frac{mass}{molar\text{ mass}}`

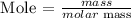
Recall, that the molar mass of water is 18.0 g/mol

`\begin{gathered} \text{ 2.505 = }(mass)/(18) \\ \text{ cross multiply} \\ \text{ Mass = 2.505 }*\text{ 18} \\ \text{ Mass = 45.09 g} \end{gathered}`

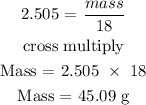
Therefore, the maximum amount of water produced is 45.09 g H20