Question

how many distinct committees of 12 people can be formed if the members are drawn from a pool of 18 people? Factorials may ne used to express the answer.

Answer 1

Answer:

18564 distinct committee of 12 can be formed

In factorial form:

`(18!)/(6!12!)`Explanations:

Note that:

`\text{nCr = }(n!)/((n-r)!r!)`

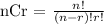
The total number of people, n = 18

The number of people to be selected = 12

The number of distinct committee of 12 people that can be selected from 18 people will be:

`\begin{gathered} 18C12\text{ = }(18!)/((18-12)!12!) \\ 18C12\text{ = }(18!)/(6!12!) \\ 18C12\text{ = }(18*17*16*15*14*13*12!)/(12!*6*5*4*3*2*1) \\ 18C12\text{ = }(18*17*16*15*14*13)/(6*5*4*3*2*1) \\ 18C12\text{ = }(13366080)/(720) \\ 18C12\text{ = }18564 \end{gathered}`

18564 committee of 12 can be formed

This can be written in factorial form as:

`(18!)/(6!12!)`