Question

Steve can complete the 100m dash in 10 seconds while Paul can run it in 12 seconds. How does Steve's time compare to Paul's?

A. Steve is 5∕6 as fast as Paul
B. Steve is 5∕6 slower than Paul
C. Steve is 1∕2 as fast as Paul
D. Steve is 1∕2 slower than Paul



a survey in which 400 people were asked to identify the TV channel on which they preferred to watch the evening news.

How many more people preferred WWCN with 41% than WANR with 22%?
A. 164
B. 76
C. 236
D. 68

Answer 1

Q-1 The correct option is A) Steve is 5∕6 as fast as Paul

Q-2 The correct option is 76.

Explanation:

Consider the provided information.

Q-1

Steve can complete the 100m dash in 10 seconds while Paul can run it in 12 seconds.

Since, the distance for both are same,

`\frac{\text{Steve's time}}{\text{Paul's time}}=(10)/(12)=(5)/(6)\\\text{Steve's time}=(5)/(6)\text{ of Paul's time}}`

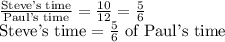
Hence, Steve's time is 5⁄6 of the time taken by Paul.

Therefore, the correct option is A) Steve is 5∕6 as fast as Paul

Q-2 a survey in which 400 people were asked to identify the TV channel on which they preferred to watch the evening news.

WWCN got 41% and WANR got 22%

For WWCN

41% of 400 is:
`(41)/(100) * 400=164`

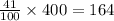
That means 164 people preferred WWCN.

For WANR

22% of 400 is:
`(22)/(100) * 400=88`

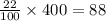
That means 88 people preferred WANR.

We need to find how many more people preferred WWCN

For this subtract both the values: 164-88=76

Thus, 76 more people preferred WWCN

Hence, the correct option is 76.

Answer 2

So, Steve's time in a ratio to Paul's time:



`(Steven's time)/(Pauls's time) = (10)/(12) = (5)/(6) .` So Steven's time is
`(5)/(6)` times shorter, that is
"Steven is
`(5)/(6)` times faster than Paul (I find the phrasing "as fast as" problematic though)

In the second question 41% of 400, which is 4*41=164 people chose WWCN and 22% chose WANR, that is 22%*400=4*22=88.

And the difference is 76 people! ( 164-88=76)B)