Given:
The trigonometric ratios are given as,
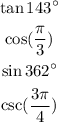
The objective is to find out which of these expressions is positive or negative.
Step-by-step explanation:
Consider the first expression and convert it as,
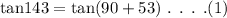
Using the trigonometric identities,
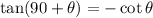
The equation (1) can be written as,
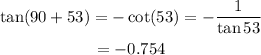
Thus, tan(143°) is a negative expression.
Consider the second trigonometric expression.
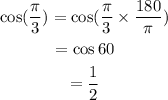
Thus, cos (π/3) is a positive expression.
Consider the third trigonometric expression.
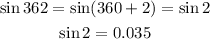
Thus, sin 362° is a positive expression.
Consider the fourth expression.
![undefined]()