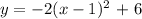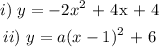
Step-by-step explanation:
i) The equation of parabola is given as:
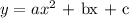
To get the equation of this parabola using the formula above, we will pick any three points on the line. Substitute these points in the formula to get a, b, and c
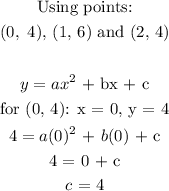
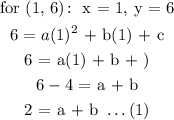
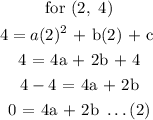
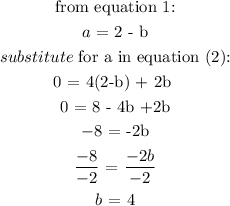
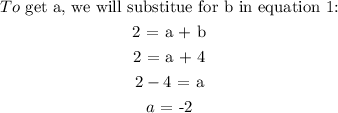
Substittute for a, b and c in the equation we were given
The equation of the graph becomes:
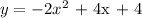
ii) Equation of a parabola in vertex form is given as:
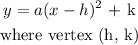
The vertex of the grap is the tip of the parabola. The tip in this case is at x = 1, y = 6
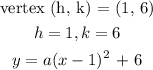
To get a, we will pick a point on the parabola:

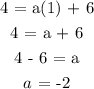
The equation in vertex form becomes: