Question

In the laboratory, a ball is dropped onto a force-sensing platform several times, each time hitting a different surface (foam, feathers, clay, etc.). The momentum of the ball changes by the same amount in each trial; in each trial, the average scale reading is F, and the time of collision t are measured. What quantities would need to be graphed to exhibit a straight-line relationship

Answer 1

Graphing the momentum against the change in moment yields a linear relationship.

Step-by-step explanation:

This is an impulse experiment,

I = ∫ F .dt

where the force and time of the collision are measured, therefore if we assume an average force the integral reduces to

I = F t

Furthermore, the momentum is equal to the change in moment of the ball, this change in moment can be found using the energy relations measuring the height of the ball and calculating its speed, in the two intervals for the descent and for the exit, possibly the heights are different so the moment change is different from zero.

Starting point. Higher

Em₀ = U = mgh

Lower end point, just before hitting the scale

`Em_(f)` = K = ½ m v²

in the path in the air there is no friction

Em₀ = Em_{f}

m g h = ½ m v²

v =
`√(2gh)`

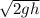
this height is different for the descent and ascent of the ball, so we have two moments

Δp =
`p_(f)` - p₀

Δp = m (v_{f} -v₀)

therefore we have the relationship

I = Δp

Graphing the momentum against the change in moment yields a linear relationship.