Question

A crow is flying horizontally with a constant speed of 2.70m/s when it releases a claim from its beak. The clan lands on the rocky Beach 2.10s later. Just before the clam lands, what is (a) its horizontal component of velocity and (b) its vertical component of velocity? (c) How would your answers to parts (a) and (b) change if the speed of the crow were increased? Explain.

Answer 1

Given:

Speed = 2.70 m

Time, t = 2.10 seconds

Let's solve for the following:

• (a) The horizontal component of the velocity.

To find the horizontal component, apply the formula:

`V_(ox)=V_o\cos \theta`

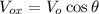
Where:

Vo is the initial speed = 2.70 m

θ = 0 degrees

Hence, we have:

`\begin{gathered} V_(ox)=2.70\cos 0 \\ \\ V_(ox)=2.7\text{ m/s} \end{gathered}`

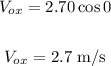
The horizontal component of the velocity just before it lands is 2.70 m/s.

• (b) The vertical component of the velocity.

To find the vertical component, apply the formula:

`V_(oy)=V_(0y)-gt=\text{V}_(oy)\text{ sin}\Theta-gt`

Where:

g is the acceleration due to gravity = 9.8 m/s²

t is the time = 2.10 s

Hence, we have:

`\begin{gathered} V_(oy)=V_(oy)\sin \theta-gt \\ \\ V_(oy)=2.70\sin 0-9.8(2.10) \\ \\ V_(oy)=0-20.58 \\ \\ V_(oy)=-20.58\text{ m/s} \end{gathered}`

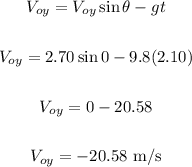
The vertical component of the velocity just before it lands is -20.58 m/s.

(c) Here, the initial speed is equal to the constant horizontal speed.

Therefore, in part (a) the horizontal component will increase in the x-direction if the speed of the crow is increased.

The initial vertical velocity is 0 m/s in both cases.

Therefore, in part (b) the vertical component will remain constant.

ANSWER:

(a) 2.70 m/s

(b) -20.58

(c) In part (a) the horizontal component will increase, while in part (b) the vertical component will remain constant.