Question

I’m a bit lost when the numbers are not the same

Answer 1

we have the expression

`3x^5\cdot8x^3=(3\cdot8)\cdot x^((5+3))=24x^8`

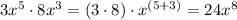
the Pythagorean theorem, states that, in any right triangle

`c^2=a^2+b^2`

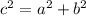
where

c is the hypotenuse of the right triangle

a and b are the legs of the triangle (a and b are perpendicular sides)

Problem N1

hypotenuse ------> c

the opposite side to given angle -----> a

the adjacent side to given angle -----> b

Problem N 2

hypotenuse -----> d

the opposite side to given angle ----> f

the adjacent side to given angle ----> e

In this picture, we have a right triangle

the hypotenuse is always the greater side -------> c

the legs a and b are always the perpendicular sides

If the reference angle is alpha

then

the adjacent side is a and the opposite side is b

If the reference angle is beta

then

the adjacent side is b and the opposite side is a

in both cases, the hypotenuse is always the same (c)