Question

For today’s lunch, a school cafeteria’s budget allows it to purchase at most 60 cans of beans and 45 cans of corn. 1 can of beans feeds 5 students, and 1 can of corn feeds 6 students. Each student will have beans or corn, but not both, and there will be a maximum of 420 students at lunch. If a can of beans cost $2.00 and a can of corn cost $3.00, what is the maximum amount of money required to feed all of the students either beans or corn?

A: $180

B: $195

C: $210

D: $225

Answer 1

I would go with B, one hundred ninety five dollars. Hope that this would help you..

Answer 2

Option B.

Explanation:

Let x be the number of cans of beans and y be the number of cans of corn.

Cafeteria’s budget allows it to purchase at most 60 cans of beans and 45 cans of corn.

`x\leq 60`

`y\leq 45`

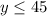
1 can of beans feeds 5 students, and 1 can of corn feeds 6 students. Each student will have beans or corn, but not both, and there will be a maximum of 420 students at lunch.

`5x+6y\leq 420`

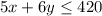
Can of beans cost $2.00 and a can of corn cost $3.00.

Objective function, Z=2x+3y

The required linear programming problem is

Objective function, Z=2x+3y

Subject to the constraints

`x\leq 60`

`y\leq 45`

`5x+6y\leq 420`

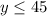
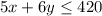
`x\geq 0, y\geq 0` (Only 1st quadrant)

Draw the graph of these constraints as shown below.

The verities of common shaded region are (0,45), (30,45), (60,20), (60,0), (0,0).

Points Z=2x+3y

(0,0) 0

(0,45) 135

(30,45) 195

(60,20) 180

(60,0) 120

The maximum amount of money required to feed all of the students either beans or corn is $195.

Number of cans of beans = 30

Number of cans of corn = 45

Therefore, the correct option is B.