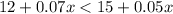Question

A telephone company offers two plans with per-minute charges. Plan A involves a monthly rental of $12, and call charges at 7¢ per minute. Plan B involves a monthly rental of $15, and call charges at 5¢ per minute.

Write an inequality in terms of the number of minutes which shows when Plan A is less expensive than Plan B. Solve the inequality, showing the steps in your work.

Answer 1

7m+12<5m+15
7m-5m+12<5m-5m+15
2m+12<15
2m+12-12<15-12
2m<3
2m/2<3/2
m<3/2

Answer 2

`12+0.07x< 15+0.05x`

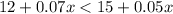
Explanation:

Let x be the no. of minutes

Plan A

Monthly rental = $12

Call charges for 1 minute = 7¢

1 cents = 0.01 dollars

So, Call charges for 1 minute = $0.07

Call charges for x minutes = 0.07 x

Total cost of Plan A = 12+0.07x

Plan B

Monthly rental = $15

Call charges for 1 minute = 5¢

1 cents = 0.01 dollars

So, Call charges for 1 minute = $0.05

Call charges for x minutes = 0.05 x

Total cost of Plan B = 15+0.05x

An inequality in terms of the number of minutes which shows when Plan A is less expensive than Plan B=
`12+0.07x< 15+0.05x`

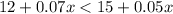
Solving the inequality :

`0.07x-0.05x< 15-12`

`0.02x< 3`

`x<(3)/(0.02)`

`x<150`

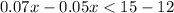
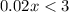
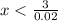
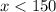
So, the no. of minutes must be less than 150 for Plan A to be less expensive than Plan B

Hence an inequality in terms of the number of minutes which shows when Plan A is less expensive than Plan B is
`12+0.07x< 15+0.05x`