Question

Verify each identity. cos^2x(1 – tan^2x) = cos 2x

Answer 1

Here, we want to prove that the right hand side of the equation equals the left hand side

We shall be moving from left to right to prove this

We proceed as follows;

Mathematically;

`\begin{gathered} \text{tan}^2x=sec^2x-1 \\ \\ \end{gathered}`

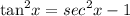
We replace this with the tan squared x in the bracket

Thus, we have the following;

`\begin{gathered} \cos ^2x(1-(\sec ^2x-1) \\ =cos^2x(1-\sec ^2x+1) \\ =cos^2x(2-\sec ^2x) \\ =2cos^2x-(cos^2x\text{ }* sec^2x) \end{gathered}`

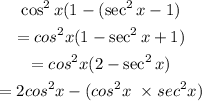
Kindly recall that;

`\begin{gathered} \cos \text{ x = }\frac{1}{\sec \text{ x}} \\ \\ \text{Thus;} \\ \cos ^2x\text{ }* sec^2x\text{ = 1} \end{gathered}`

Hence, we have the following;

`2\cos ^2x-1`

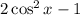
This is what we have on the left hand side

Let us simplify the right hand side too

This will be;