Question

Please give a worked explanation! Thanks :)

Answer 1

a) We need a common denominator to be able to subtract the fractions, so by multiplying both the numerator and the denominator of each fraction by the denominator of the other.

`(x + 2)/(x + 2) ( (3)/(x)) - (x)/(x) ( (5)/(x + 2) )`
Then simplify the fraction:

`(6 + 3x)/(x^(2) + 2x) - (5x)/(x^(2) + 2x)`
Then you can just subtract the nominators from each other, but leave the denominator as it is

`((6 + 3x) - 5x)/(x^(2) + 2x)`
to get:

`(6 - 2x)/(x^(2) + 2x)`
and then you can simplify to get the final answer:

`(2(3 - x))/(x(x + 2))`

b) you need to have the number inside the root the same to add or subtract:

`√(2(9)) - √(2) + √(2(36))`
Then you can 'take out' the numbers that square root easily:

`3√(2) - √(2) + 6√(2)`
now you can just add and subtract using the whole numbers outside the root of 2 ( since 2 is a surd):

`8√(2)`

Answer 2

When you add any fractions, you need to find a common denominator. In this case they have no common factors so you just multiply them together. First multiply the first fraction by
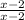
`(x - 2)/(x - 2)` which gets you
`(3x - 6)/( x^(2) - 2x)`. Then multiply the second fraction by
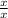
`(x)/(x)` to get
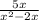
`(5x)/( x^(2) - 2x)`. Now you can add them together to get
`(-2x - 6)/( x^(2) - 2x)`.

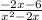
(b)
`√(18) = √(9 * 2) = 3 √(2)`

`√(72) = √(36 * 2) = 6 √(2)`
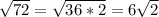
now you can pull out root 2 and get
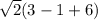
`√(2)(3 - 1 + 6)` which equals
`8 √(2)`