Question

Find the coordinates of Point P on line segment AB, where point P partitions AB at a 2:3 ratio. A(-3,-4) and B(2,6)

Answer 1

We are asked to find the coordinates of a point in a line segment that lies at a 2:3 ratio.

If the ratio is a:b, then the coordinates of a point that lies at that ratio is:

`P_x=x_1+((a)/(a+b))(x_2-x_1)`
`P_y=y_1+((a)/(a+b))(y_2-y_1)`

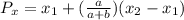
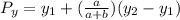
Where

`\begin{gathered} (x_1,y_1)\text{ } \\ (x_2,y_2) \end{gathered}`

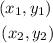
Are the extreme points.

First, we will find the "x" coordinate of the point by finding the length of the segment of the line that lies in the "x" direction by subtracting the "x" coordinates of the given points, like this:

`D_x=2-(-3)=5`

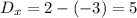
The "x" coordinate of P must lie at 2:3 ratio of this distance, that is, it must lie at the following point

`P_x=-3+5((2)/(2+3))=-1`

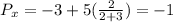
To find the "y" coordinate we do a similar process

`D_y=6-(-4)=10`

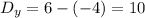
We find the "y" coordinate

`P_y=-4+10((2)/(2+3))=0`

The answer is P=(-1,0)