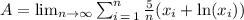Answer:
To find the expression of the area under the graph f as limit,
Given that,
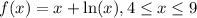
we get,
Consider the small rectangles in the area under the graph f, such that length is f(x) at x point and width is
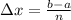
Where a and b are the end points and the n represents the number of partitions.(for n tends to infinity we can get the accurate area under the graph f)
The area of the graph under f is given by,
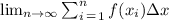
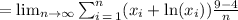
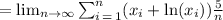
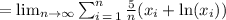
Answer is: