Question

A box with a height (x+5) has a square base with side x. A second box with height (x+2) has a square base with side (x+5). If the two boxes have the same volume, find the value of x

Answer 1

x = -1.43

Explanation :

As given ,

The first box has a height (x+5) has a square base with side x

So, the Length and Breadth of the box are x and x respectively.

Now,

The volume of first box = Length×Breadth×Height

= (x).(x).(x+5)

= x²(x+5)

⇒The volume of first box = x²(x+5)

Now,

Given that , the second box with height (x+2) has a square base with side (x+5).

So, the Length and Breadth of the box are (x+5) and (x+5) respectively.

Now,

The volume of second box = Length×Breadth×Height

= (x+5). (x+5).(x+2)

= (x+5)²(x+2)

⇒The volume of second box = (x+5)²(x+2)

Now,

Given that, the two boxes have the same volume

⇒x²(x+5) = (x+5)²(x+2)

⇒x² = (x+5)(x+2)

⇒x² = x² + 2x + 5x + 10

⇒x² - x² = 7x + 10

⇒0 = 7x + 10

⇒ 7x = -10

⇒ x = -
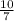`(10)/(7)` = -1.43

⇒ x = -1.43

As volume of first box = x²(x+5) = (-1.43)²(-1.43+5) = 7.30 ≈ 7

As volume of second box = (x+5)²(x+2) = (-1.43+5)²(-1.43+2) = 7.26 ≈ 7

At x = -1.43, Volume of both the boxes are same.