Question

The World-War II battleship U.S.S Massachusetts used 16-inch guns whose barrel lengths were 15 m long. The shells each of mass 1250 kg when fired, had a muzzle velocity of 750 m/s. Assuming a constant force, determine the explosive force experienced by the shell inside the barrel. Start from a fundamental principle.

Answer 1

The explosive force experienced by the shell inside the barrel is 23437500 newtons.

Step-by-step explanation:

Let suppose that shells are not experiencing any effect from non-conservative forces (i.e. friction, air viscosity) and changes in gravitational potential energy are negligible. The explosive force experienced by the shell inside the barrel can be estimated by Work-Energy Theorem, represented by the following formula:

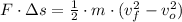`F\cdot \Delta s = (1)/(2)\cdot m \cdot (v_(f)^(2)-v_(o)^(2))` (1)

Where:

`F` - Explosive force, measured in newtons.

`\Delta s` - Barrel length, measured in meters.

`m` - Mass of the shell, measured in kilograms.

`v_(o)`,
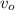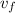`v_(f)` - Initial and final speeds of the shell, measured in meters per second.

If we know that
`m = 1250\,kg`,
`v_(o) = 0\,(m)/(s)`,
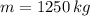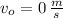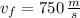`v_(f) = 750\,(m)/(s)` and
`\Delta s = 15\,m`, then the explosive force experienced by the shell inside the barrel is:

`F = (m\cdot (v_(f)^(2)-v_(o)^(2)))/(2\cdot \Delta s)`

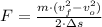
`F = ((1250\,kg)\cdot \left[\left(750\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right])/(2\cdot (15\,m))`

`F = 23437500\,N`

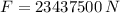
The explosive force experienced by the shell inside the barrel is 23437500 newtons.