Given:
Margin of error = 0.04
Confidence level = 95%
Let's answer the following questions:
• (A). Assume that nothing is known about the percentage to be estimated.
Since we are to assume that nothing about the percentage is know, we have:
p = q = 0.5
E = 0.04
Given a 95% confidence interval, we have:
Significance level = 1 - 0.95 = 0.05
Using the z-table, for a two tailed test, we have:

Hence, the sample size will be:
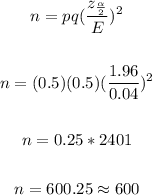
Therefore, the required sample size is 600
• (b,). Here, we have the following:
p = 60% = 0.60
q = 1 - p = 1 - 0.60 = 0.40
95% confidence interval, z = 1.96
E = 0.04
To solve for n, we have:
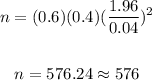
Here, the sample size is 576
(C).
No, the added knowledge in part B does not have much of an effect on the sample size.
It only slightly reduces the sample size.
ANSWER:
• (A). 600
,
• (B). 576
,
• (C). No, it only slightly reduces the sample size.