Question

A model rocket is launched from a roof into a large field. The path of the rocket can be modeled by the equation

y equals negative 0.04x squared plus 8.3x plus 4.3, where x is the horizontal distance, in meters, from the starting point on the roof and y is the height, in meters, of the rocket above the ground. How far horizontally from its starting point will the rocket land? Round your answer to the nearest hundredth meter. (1 point)
208.02 m
416.03 m
0.52 m
208.19 m

Answer 1

ok

y=-0.04x^2+8.3x+4.3
when the rocket reaches the ground (when height=0, ie when y=0), then the rocket will land, find the x coordinate

set y=0
0=-0.04x^2+8.3x+4.3
use quadratic formula
if you have ax^2+bx+c=0, then
x=
`\frac{-b+/- \sqrt{b^(2)-4ac} }{2a}`
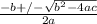
a=-0.04
b=8.3
c=4.3
x=
`\frac{-8.3+/- \sqrt{8.3^(2)-4(-0.04)(8.3)} }{2(-0.04)}`
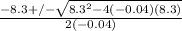
x=208.017 or -0.516785
xrepresents horizontal distance
you cannot have a negative horizontal distance unless you fired and theh wind blew it backwards
therefor x=280.017 is the answer
208.02 m