Solution
The function given is

- A polynomial has the following properties:
1. The exponent of the variable must be a natural number or a positive integer.
2. The coefficients and constant can be any real number.
3. The leading term is the term on which its variable has the highest exponent
- The standard form of any polynomial is given as
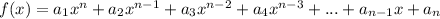
- The equation given has a variable of x. This variable has 1 as its highest exponent. While the coefficients and constants of the equation are real numbers.
- This means that it satisfies all the properties of a polynomial.
- Thus, we have the standard form of the polynomial to be:
