Question

Question 20 Determine if the function is a polynomial function. If it is state the degree. If it is not tell why not. Write the polynomial in standard form. Then identify the leading term and constant term.

Answer 1

The function given is

`h(x)=3-(1)/(2)x`

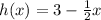
- A polynomial has the following properties:

1. The exponent of the variable must be a natural number or a positive integer.

2. The coefficients and constant can be any real number.

3. The leading term is the term on which its variable has the highest exponent

- The standard form of any polynomial is given as

`f(x)=a_1x^n+a_2x^(n-1)+a_3x^(n-2)+a_4x^(n-3)+...+a_(n-1)x+a_n`

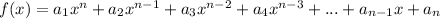
- The equation given has a variable of x. This variable has 1 as its highest exponent. While the coefficients and constants of the equation are real numbers.

- This means that it satisfies all the properties of a polynomial.

- Thus, we have the standard form of the polynomial to be:

`\begin{gathered} f(x)=-(1)/(2)x+3 \\ \\ \text{ The Leading Coefficient is:} \\ -(1)/(2) \\ \\ \text{ The constant term is:} \\ 3 \end{gathered}`