Question

Determine the input value for which the statementf(x) = g(x) is true.From the graph, the input value is approximately ____f(x) = 3 and g(x) = 3/2x-23 = 3/2x-25 = 3/2xThe x-value at which the two functions' values areequal is ____

Answer 1

This question is about the intersection of functions.

When we say that two functions are equal at a certain value, it means their graph meet at that point.

In this case, we have two functions

`f(x)=3,g(x)=(3)/(2)x-2`

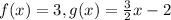
To find the exact value where these functions are equal, we need to make them equal

`f(x)=g(x)`

Replacing the functions, we have

`3=(3)/(2)x-2`

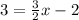
Now, we solve for x

`3+2=(3)/(2)x\rightarrow5=(3)/(2)x\rightarrow(10)/(3)=x\rightarrow x\approx3.33333\ldots`

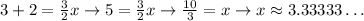
This means the x-value at which the two functions' values are equal is 10/3, or 3.333...

Additionally, the y-value at which the two function's values are equal is 3.

Therefore, these functions are equal at point (10/3 , 3).